Random Lattice Generators Are Not Bad
import qmcpy as qp
import numpy as np #basic numerical routines in Python
import time #timing routines
from matplotlib import pyplot; #plotting
pyplot.rc('font', size=16) #set defaults so that the plots are readable
pyplot.rc('axes', titlesize=16)
pyplot.rc('axes', labelsize=16)
pyplot.rc('xtick', labelsize=16)
pyplot.rc('ytick', labelsize=16)
pyplot.rc('legend', fontsize=16)
pyplot.rc('figure', titlesize=16)
#a helpful plotting method to show increasing numbers of points
def plot_successive_points(distrib,ld_name,first_n=64,n_cols=1,pt_clr='bgkcmy',
xlim=[0,1],ylim=[0,1],coord1 = 0,coord2 = 1):
fig,ax = pyplot.subplots(nrows=1,ncols=n_cols,figsize=(5*n_cols,5.5))
if n_cols==1: ax = [ax]
last_n = first_n*(2**n_cols)
points = distrib.gen_samples(n=last_n)
for i in range(n_cols):
n = first_n
nstart = 0
for j in range(i+1):
n = first_n*(2**j)
ax[i].scatter(points[nstart:n,coord1],points[nstart:n,coord2],color=pt_clr[j])
nstart = n
ax[i].set_title('n = %d'%n)
ax[i].set_xlim(xlim); ax[i].set_xticks(xlim); ax[i].set_xlabel('$x_{i,%d}$'%(coord1+1))
ax[i].set_ylim(ylim); ax[i].set_yticks(ylim); ax[i].set_ylabel('$x_{i,%d}$'%(coord2+1))
ax[i].set_aspect((xlim[1]-xlim[0])/(ylim[1]-ylim[0]))
fig.suptitle('%s Points'%ld_name)
Lattice Declaration and the gen_samples function
lat = qp.Lattice()
help(lat.__init__)
Help on method __init__ in module qmcpy.discrete_distribution.lattice.lattice:
__init__(dimension=1, randomize=True, order='natural', seed=None, generating_vector='lattice_vec.3600.20.npy', d_max=None, m_max=None) method of qmcpy.discrete_distribution.lattice.lattice.Lattice instance
Args:
dimension (int or ndarray): dimension of the generator.
If an int is passed in, use sequence dimensions [0,...,dimensions-1].
If a ndarray is passed in, use these dimension indices in the sequence.
randomize (bool): If True, apply shift to generated samples.
Note: Non-randomized lattice sequence includes the origin.
order (str): 'linear', 'natural', or 'mps' ordering.
seed (None or int or numpy.random.SeedSeq): seed the random number generator for reproducibility
generating_vector (ndarray, str or int): generating matrix or path to generating matrices.
ndarray should have shape (d_max).
a string generating_vector should be formatted like
'lattice_vec.3600.20.npy' where 'name.d_max.m_max.npy'
an integer should be an odd larger than 1; passing an integer M would create a random generating vector supporting up to 2^M points.
M is restricted between 2 and 26 for numerical percision. The generating vector is [1,v_1,v_2,...,v_dimension], where v_i is an integer in {3,5,...,2*M-1}.
d_max (int): maximum dimension
m_max (int): 2^m_max is the max number of supported samples
Note:
d_max and m_max are required if generating_vector is a ndarray.
If generating_vector is an string (path), d_max and m_max can be taken from the file name if None
help(lat.gen_samples)
Help on method gen_samples in module qmcpy.discrete_distribution.lattice.lattice:
gen_samples(n=None, n_min=0, n_max=8, warn=True, return_unrandomized=False) method of qmcpy.discrete_distribution.lattice.lattice.Lattice instance
Generate lattice samples
Args:
n (int): if n is supplied, generate from n_min=0 to n_max=n samples.
Otherwise use the n_min and n_max explicitly supplied as the following 2 arguments
n_min (int): Starting index of sequence.
n_max (int): Final index of sequence.
return_unrandomized (bool): return samples without randomization as 2nd return value.
Will not be returned if randomize=False.
Returns:
ndarray: (n_max-n_min) x d (dimension) array of samples
Note:
Lattice generates in blocks from 2**m to 2**(m+1) so generating
n_min=3 to n_max=9 requires necessarily produces samples from n_min=2 to n_max=16
and automatically subsets. May be inefficient for non-powers-of-2 samples sizes.
Driver code
lat = qp.Lattice(dimension = 2,randomize= True, generating_vector=21, seed = 120)
print("Basic information of the lattice:")
print(lat)
print("\nA sample lattice generated by the random generating vector: ")
n = 16 #number of points in the sample
print(lat.gen_samples(n))
Basic information of the lattice:
Lattice (DiscreteDistribution Object)
d 2^(1)
dvec [0 1]
randomize 1
order natural
gen_vec [ 1 249531]
entropy 120
spawn_key ()
A sample lattice generated by the random generating vector:
[[0.34548142 0.46736834]
[0.84548142 0.96736834]
[0.59548142 0.21736834]
[0.09548142 0.71736834]
[0.47048142 0.84236834]
[0.97048142 0.34236834]
[0.72048142 0.59236834]
[0.22048142 0.09236834]
[0.40798142 0.15486834]
[0.90798142 0.65486834]
[0.65798142 0.90486834]
[0.15798142 0.40486834]
[0.53298142 0.52986834]
[0.03298142 0.02986834]
[0.78298142 0.27986834]
[0.28298142 0.77986834]]
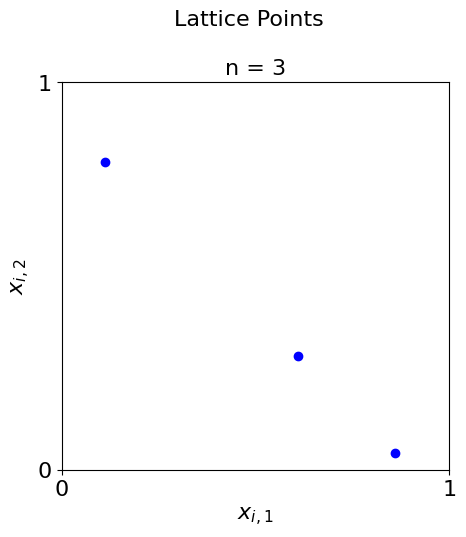
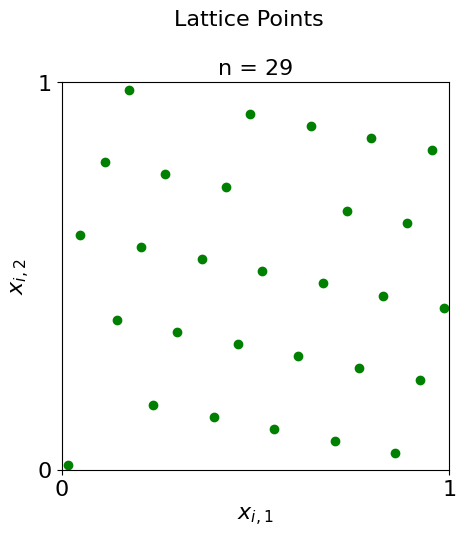
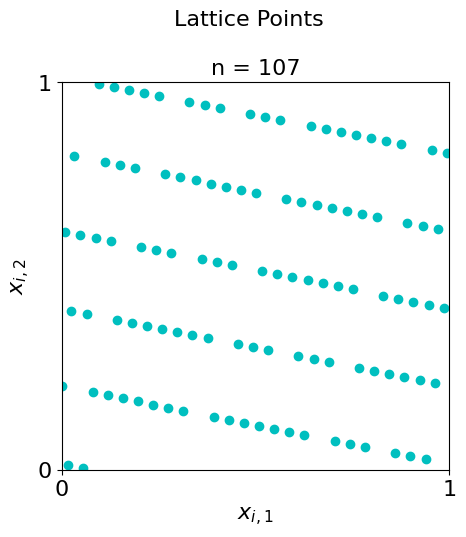
Plots of lattices
#Here the sample sizes are prime numbers
lat = qp.Lattice(dimension=2,generating_vector= 16,seed = 136)
primes = [3,29,107,331,773]
for i in range(0,5):
plot_successive_points(distrib = lat,ld_name = "Lattice",first_n=primes[i],pt_clr="bgcmr"[i])
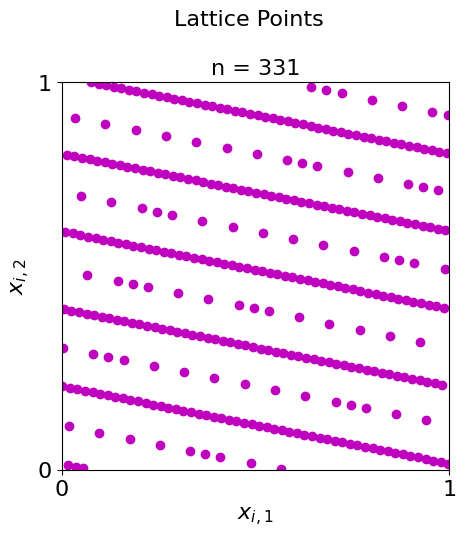
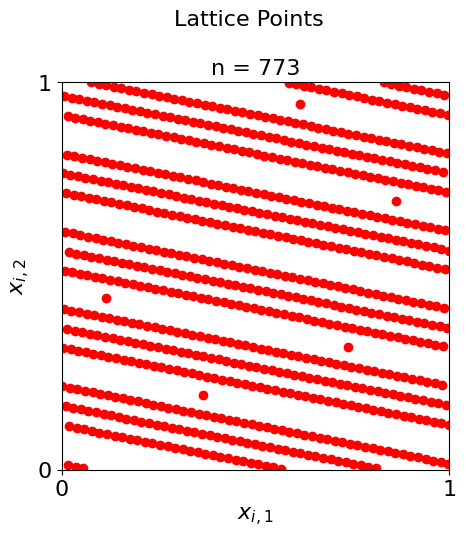
Integration
Runtime comparison bewteen radnom generator and hard-conded generator
import warnings
warnings.simplefilter('ignore')
d = 5 #coded as parameters so that
tol = 1E-3 #you can change here and propagate them through this example
data_random = qp.CubQMCLatticeG(qp.Keister(qp.Gaussian(qp.Lattice(d,generating_vector = 26), mean = 0, covariance = 1/2)), abs_tol = tol).integrate()[1]
data_default = qp.CubQMCLatticeG(qp.Keister(qp.Gaussian(qp.Lattice(d), mean = 0, covariance = 1/2)), abs_tol = tol).integrate()[1]
print("Integration data from a random lattice generator:")
print(data_random)
print("\nIntegration data from the default lattice generator:")
print(data_default)
Integration data from a random lattice generator:
LDTransformData (AccumulateData Object)
solution 1.135
comb_bound_low 1.134
comb_bound_high 1.135
comb_flags 1
n_total 2^(17)
n 2^(17)
time_integrate 0.637
CubQMCLatticeG (StoppingCriterion Object)
abs_tol 0.001
rel_tol 0
n_init 2^(10)
n_max 2^(35)
Keister (Integrand Object)
Gaussian (TrueMeasure Object)
mean 0
covariance 2^(-1)
decomp_type PCA
transform Gaussian (TrueMeasure Object)
mean 0
covariance 2^(-1)
decomp_type PCA
Lattice (DiscreteDistribution Object)
d 5
dvec [0 1 2 3 4]
randomize 1
order natural
gen_vec [ 1 10247129 59899927 37429227 4270157]
entropy 179627174552261816434188931064794162705
spawn_key ()
Integration data from the default lattice generator:
LDTransformData (AccumulateData Object)
solution 1.136
comb_bound_low 1.136
comb_bound_high 1.137
comb_flags 1
n_total 2^(17)
n 2^(17)
time_integrate 0.631
CubQMCLatticeG (StoppingCriterion Object)
abs_tol 0.001
rel_tol 0
n_init 2^(10)
n_max 2^(35)
Keister (Integrand Object)
Gaussian (TrueMeasure Object)
mean 0
covariance 2^(-1)
decomp_type PCA
transform Gaussian (TrueMeasure Object)
mean 0
covariance 2^(-1)
decomp_type PCA
Lattice (DiscreteDistribution Object)
d 5
dvec [0 1 2 3 4]
randomize 1
order natural
gen_vec [ 1 182667 469891 498753 110745]
entropy 286106574132041199018132344291732219476
spawn_key ()
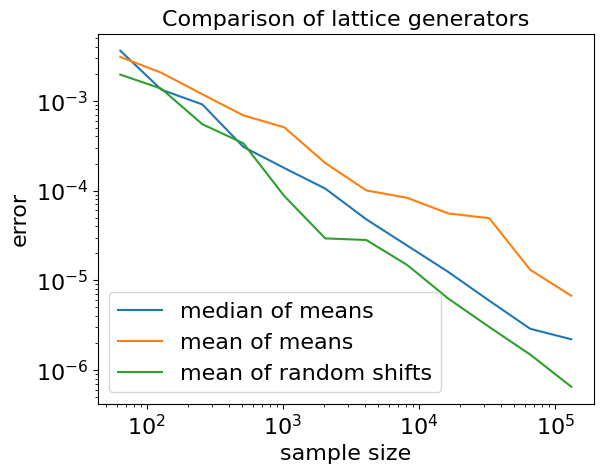
Mean vs. Median as a function of the sample size plot
#mean vs. median plot
import qmcpy as qp
import numpy as np
import matplotlib.pyplot as plt
d = 2
N_min = 6
N_max = 18
N_list = 2**np.arange(N_min,N_max)
r = 11
num_trials = 25
error_median = np.zeros(N_max - N_min)
error_mean = np.zeros(N_max - N_min)
error_mean_onegen = np.zeros(N_max - N_min)
for i in range(num_trials):
y_median = []
y_mean = []
y_mean_one_gen = []
print(i)
list_of_keister_objects_random = []
list_of_keister_objects_default = []
y_randomized_list = []
y_default_list = []
for k in range(r):
lattice = qp.Lattice(generating_vector = 26,dimension=d)
keister = qp.Keister(lattice)
list_of_keister_objects_random.append(keister)
x = keister.discrete_distrib.gen_samples(N_list.max())
y = keister.f(x)
y_randomized_list.append(y)
keister = qp.Keister(qp.Lattice(d))
list_of_keister_objects_default.append(keister)
x = keister.discrete_distrib.gen_samples(N_list.max())
y = keister.f(x)
y_default_list.append(y)
for N in N_list:
y_median.append(np.median([np.mean(y[:N]) for y in y_randomized_list]))
y_mean_one_gen.append(np.mean([np.mean(y[:N]) for y in y_default_list]))
y_mean.append(np.mean([np.mean(y[:N]) for y in y_randomized_list]))
answer = keister.exact_integ(d)
error_median += abs(answer-y_median)
error_mean += abs(answer-y_mean)
error_mean_onegen += abs(answer-y_mean_one_gen)
error_median /= num_trials
error_mean /= num_trials
error_mean_onegen /= num_trials
plt.loglog(N_list,error_median,label = "median of means")
plt.loglog(N_list,error_mean,label = "mean of means")
plt.loglog(N_list,error_mean_onegen,label = "mean of random shifts")
plt.xlabel("sample size")
plt.ylabel("error")
plt.title("Comparison of lattice generators")
plt.legend()
plt.savefig("./meanvsmedian.png")
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24