import matplotlib.pyplot as plt
import numpy as np
import qmcpy as qp
seed = 7
Comparison of multilevel (Quasi-)Monte Carlo for an Asian option problem
Compute the exact value of the Asian option with single level QMC, for an increasing number of time steps:
for level in range(5):
aco = qp.AsianOption(qp.Sobol(2*2**level, seed=seed), volatility=.2, start_price=100, strike_price=100, interest_rate=.05)
approx_solution, data = qp.CubQMCSobolG(aco, abs_tol=1e-4).integrate()
print("Asian Option true value (%d time steps): %.5f (to within 1e-4)"%(2*2**level, approx_solution))
Asian Option true value (2 time steps): 5.63591 (to within 1e-4)
Asian Option true value (4 time steps): 5.73171 (to within 1e-4)
Asian Option true value (8 time steps): 5.75526 (to within 1e-4)
Asian Option true value (16 time steps): 5.76113 (to within 1e-4)
Asian Option true value (32 time steps): 5.76260 (to within 1e-4)
This function compares 4 different algorithms: Multilevel Monte Carlo
(CubMCML), Multilevel Quasi-Monte Carlo (CubQMCML), continuation
Multilevel Monte Carlo (CubMCMLCont) and Multilevel Quasi-Monte
Carlo (CubQMCMLCont):
def eval_option(option_mc, option_qmc, abs_tol):
stopping_criteria = {
"MLMC" : qp.CubMCML(option_mc, abs_tol=abs_tol, levels_max=15),
"continuation MLMC" : qp.CubMCMLCont(option_mc, abs_tol=abs_tol, levels_max=15),
"MLQMC" : qp.CubQMCML(option_qmc, abs_tol=abs_tol, levels_max=15),
"continuation MLQMC" : qp.CubQMCMLCont(option_qmc, abs_tol=abs_tol, levels_max=15)
}
levels = []
times = []
for name, stopper in stopping_criteria.items():
sol, data = stopper.integrate()
levels.append(data.levels)
times.append(data.time_integrate)
print("\t%-20s solution %-10.4f number of levels %-6d time %.3f"%(name, sol, levels[-1], times[-1]))
return levels, times
Define the Multilevel Asian options:
option_mc = qp.MLCallOptions(qp.IIDStdUniform(seed=seed), option="asian")
option_qmc = qp.MLCallOptions(qp.Lattice(seed=seed), option="asian")
Run and compare each of the 4 algorithms for the Asian option problem:
eval_option(option_mc, option_qmc, abs_tol=5e-3);
MLMC solution 5.7620 number of levels 10 time 12.119
continuation MLMC solution 5.7580 number of levels 7 time 7.775
MLQMC solution 5.7606 number of levels 8 time 55.780
continuation MLQMC solution 5.7594 number of levels 7 time 18.445
Repeat this comparison for a sequence of decreasing tolerances, with 5 different random seeds each. This will allow us to visualize the asymptotic cost complexity of each method.
repetitions = 5
tolerances = 5*np.logspace(-1, -3, num=5)
levels = {}
times = {}
for t in range(len(tolerances)):
for r in range(repetitions):
print("tolerance = %10.4e, repetition = %d/%d"%(tolerances[t], r + 1, repetitions))
levels[t, r], times[t, r] = eval_option(option_mc, option_qmc, tolerances[t])
tolerance = 5.0000e-01, repetition = 1/5
MLMC solution 5.5049 number of levels 3 time 0.006
continuation MLMC solution 5.6865 number of levels 3 time 0.008
MLQMC solution 5.7204 number of levels 3 time 0.144
continuation MLQMC solution 5.7099 number of levels 3 time 0.000
tolerance = 5.0000e-01, repetition = 2/5
MLMC solution 5.7316 number of levels 4 time 0.005
continuation MLMC solution 5.6755 number of levels 4 time 0.009
MLQMC solution 5.7196 number of levels 3 time 0.139
continuation MLQMC solution 5.7014 number of levels 3 time 0.000
tolerance = 5.0000e-01, repetition = 3/5
MLMC solution 5.6791 number of levels 3 time 0.004
continuation MLMC solution 5.8100 number of levels 3 time 0.006
MLQMC solution 5.6972 number of levels 3 time 0.142
continuation MLQMC solution 5.7100 number of levels 3 time 0.000
tolerance = 5.0000e-01, repetition = 4/5
MLMC solution 5.8077 number of levels 3 time 0.004
continuation MLMC solution 5.6728 number of levels 4 time 0.009
MLQMC solution 5.7058 number of levels 3 time 0.155
continuation MLQMC solution 5.7118 number of levels 3 time 0.000
tolerance = 5.0000e-01, repetition = 5/5
MLMC solution 5.4125 number of levels 3 time 0.004
continuation MLMC solution 5.8328 number of levels 4 time 0.009
MLQMC solution 5.6996 number of levels 3 time 0.153
continuation MLQMC solution 5.7150 number of levels 3 time 0.000
tolerance = 1.5811e-01, repetition = 1/5
MLMC solution 5.7598 number of levels 6 time 0.022
continuation MLMC solution 5.7586 number of levels 4 time 0.016
MLQMC solution 5.7358 number of levels 4 time 0.276
continuation MLQMC solution 5.7015 number of levels 3 time 0.021
tolerance = 1.5811e-01, repetition = 2/5
MLMC solution 5.6662 number of levels 6 time 0.022
continuation MLMC solution 5.7764 number of levels 4 time 0.028
MLQMC solution 5.7354 number of levels 4 time 0.237
continuation MLQMC solution 5.7456 number of levels 4 time 0.063
tolerance = 1.5811e-01, repetition = 3/5
MLMC solution 5.7615 number of levels 6 time 0.020
continuation MLMC solution 5.6784 number of levels 3 time 0.012
MLQMC solution 5.7238 number of levels 4 time 0.249
continuation MLQMC solution 5.7459 number of levels 4 time 0.069
tolerance = 1.5811e-01, repetition = 4/5
MLMC solution 5.7532 number of levels 6 time 0.022
continuation MLMC solution 5.7984 number of levels 4 time 0.016
MLQMC solution 5.7209 number of levels 4 time 0.272
continuation MLQMC solution 5.7137 number of levels 3 time 0.017
tolerance = 1.5811e-01, repetition = 5/5
MLMC solution 5.7755 number of levels 5 time 0.017
continuation MLMC solution 5.7146 number of levels 4 time 0.016
MLQMC solution 5.7429 number of levels 4 time 0.232
continuation MLQMC solution 5.7075 number of levels 3 time 0.019
tolerance = 5.0000e-02, repetition = 1/5
MLMC solution 5.7686 number of levels 7 time 0.139
continuation MLMC solution 5.7658 number of levels 6 time 0.125
MLQMC solution 5.7454 number of levels 5 time 0.412
continuation MLQMC solution 5.7357 number of levels 4 time 0.024
tolerance = 5.0000e-02, repetition = 2/5
MLMC solution 5.7597 number of levels 7 time 0.138
continuation MLMC solution 5.7266 number of levels 4 time 0.068
MLQMC solution 5.7454 number of levels 5 time 0.434
continuation MLQMC solution 5.7327 number of levels 4 time 0.025
tolerance = 5.0000e-02, repetition = 3/5
MLMC solution 5.7660 number of levels 7 time 0.144
continuation MLMC solution 5.7496 number of levels 4 time 0.104
MLQMC solution 5.7476 number of levels 5 time 0.516
continuation MLQMC solution 5.7350 number of levels 4 time 0.024
tolerance = 5.0000e-02, repetition = 4/5
MLMC solution 5.7354 number of levels 7 time 0.136
continuation MLMC solution 5.7693 number of levels 5 time 0.079
MLQMC solution 5.7501 number of levels 5 time 0.381
continuation MLQMC solution 5.7338 number of levels 4 time 0.024
tolerance = 5.0000e-02, repetition = 5/5
MLMC solution 5.7545 number of levels 7 time 0.122
continuation MLMC solution 5.7705 number of levels 5 time 0.067
MLQMC solution 5.7431 number of levels 5 time 0.385
continuation MLQMC solution 5.7446 number of levels 5 time 0.108
tolerance = 1.5811e-02, repetition = 1/5
MLMC solution 5.7596 number of levels 8 time 1.203
continuation MLMC solution 5.7656 number of levels 6 time 1.068
MLQMC solution 5.7566 number of levels 6 time 1.041
continuation MLQMC solution 5.7557 number of levels 6 time 0.369
tolerance = 1.5811e-02, repetition = 2/5
MLMC solution 5.7599 number of levels 8 time 1.327
continuation MLMC solution 5.7504 number of levels 5 time 0.860
MLQMC solution 5.7585 number of levels 7 time 1.350
continuation MLQMC solution 5.7553 number of levels 6 time 0.316
tolerance = 1.5811e-02, repetition = 3/5
MLMC solution 5.7632 number of levels 8 time 1.261
continuation MLMC solution 5.7595 number of levels 6 time 1.172
MLQMC solution 5.7545 number of levels 6 time 1.080
continuation MLQMC solution 5.7464 number of levels 5 time 0.150
tolerance = 1.5811e-02, repetition = 4/5
MLMC solution 5.7655 number of levels 8 time 1.122
continuation MLMC solution 5.7494 number of levels 6 time 1.079
MLQMC solution 5.7597 number of levels 7 time 1.148
continuation MLQMC solution 5.7476 number of levels 5 time 0.220
tolerance = 1.5811e-02, repetition = 5/5
MLMC solution 5.7635 number of levels 8 time 1.509
continuation MLMC solution 5.7565 number of levels 6 time 1.181
MLQMC solution 5.7548 number of levels 6 time 0.913
continuation MLQMC solution 5.7483 number of levels 5 time 0.140
tolerance = 5.0000e-03, repetition = 1/5
MLMC solution 5.7619 number of levels 10 time 14.429
continuation MLMC solution 5.7596 number of levels 7 time 9.738
MLQMC solution 5.7614 number of levels 8 time 6.359
continuation MLQMC solution 5.7594 number of levels 7 time 3.222
tolerance = 5.0000e-03, repetition = 2/5
MLMC solution 5.7634 number of levels 10 time 14.773
continuation MLMC solution 5.7591 number of levels 7 time 13.011
MLQMC solution 5.7610 number of levels 8 time 7.475
continuation MLQMC solution 5.7600 number of levels 7 time 3.833
tolerance = 5.0000e-03, repetition = 3/5
MLMC solution 5.7644 number of levels 10 time 17.306
continuation MLMC solution 5.7585 number of levels 8 time 13.856
MLQMC solution 5.7615 number of levels 8 time 6.449
continuation MLQMC solution 5.7588 number of levels 7 time 3.534
tolerance = 5.0000e-03, repetition = 4/5
MLMC solution 5.7617 number of levels 10 time 16.390
continuation MLMC solution 5.7583 number of levels 7 time 12.321
MLQMC solution 5.7611 number of levels 8 time 6.453
continuation MLQMC solution 5.7596 number of levels 7 time 2.596
tolerance = 5.0000e-03, repetition = 5/5
MLMC solution 5.7638 number of levels 10 time 15.755
continuation MLMC solution 5.7583 number of levels 8 time 14.382
MLQMC solution 5.7609 number of levels 8 time 7.762
continuation MLQMC solution 5.7587 number of levels 7 time 4.633
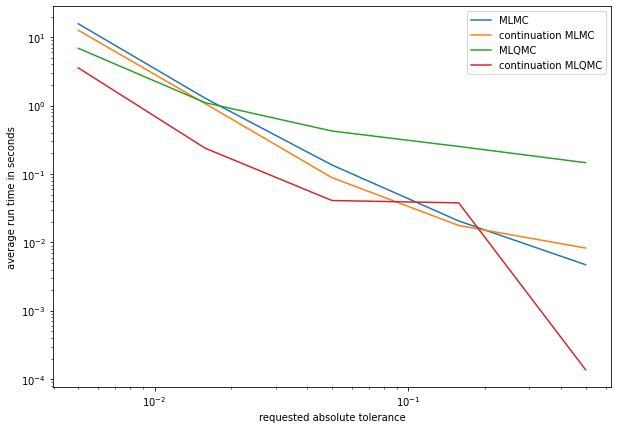
Compute and plot the asymptotic cost complexity.
avg_time = {}
for method in range(4):
avg_time[method] = [np.mean([times[t, r][method] for r in range(repetitions)]) for t in range(len(tolerances))]
plt.figure(figsize=(10,7))
plt.plot(tolerances, avg_time[0], label="MLMC")
plt.plot(tolerances, avg_time[1], label="continuation MLMC")
plt.plot(tolerances, avg_time[2], label="MLQMC")
plt.plot(tolerances, avg_time[3], label="continuation MLQMC")
plt.xscale("log")
plt.yscale("log")
plt.xlabel("requested absolute tolerance")
plt.ylabel("average run time in seconds")
plt.legend();
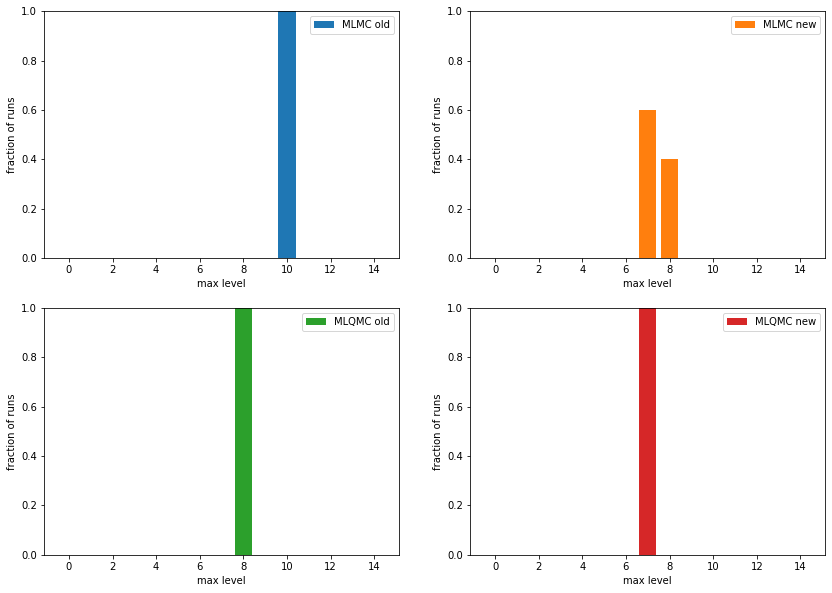
max_levels = {}
for method in range(4):
levels_rep = np.array([levels[len(tolerances)-1, r][method] for r in range(repetitions)])
max_levels[method] = [np.count_nonzero(levels_rep == level)/repetitions for level in range(15)]
plt.figure(figsize=(14,10))
plt.subplot(2,2,1); plt.bar(range(15), max_levels[0], label="MLMC old", color="C0"); plt.xlabel("max level"); plt.ylabel("fraction of runs"); plt.ylim(0, 1); plt.legend()
plt.subplot(2,2,2); plt.bar(range(15), max_levels[1], label="MLMC new", color="C1"); plt.xlabel("max level"); plt.ylabel("fraction of runs"); plt.ylim(0, 1); plt.legend()
plt.subplot(2,2,3); plt.bar(range(15), max_levels[2], label="MLQMC old", color="C2"); plt.xlabel("max level"); plt.ylabel("fraction of runs"); plt.ylim(0, 1); plt.legend()
plt.subplot(2,2,4); plt.bar(range(15), max_levels[3], label="MLQMC new", color="C3"); plt.xlabel("max level"); plt.ylabel("fraction of runs"); plt.ylim(0, 1); plt.legend();