Welcome to QMCPy
Importing QMCPy
Here we show three different ways to import QMCPy in a Python
environment. First, we can import the package qmcpy under the alias
qp.
import qmcpy as qp
print(qp.name, qp.__version__)
qmcpy 1.3
Alternatively, we can import individual objects from ‘qmcpy’ as shown below.
from qmcpy.integrand import *
from qmcpy.true_measure import *
from qmcpy.discrete_distribution import *
from qmcpy.stopping_criterion import *
Lastly, we can import all objects from the package using an asterisk.
from qmcpy import *
Important Notes
IID vs LDS
Low discrepancy (LD) sequences such as lattice and Sobol’ are not independent like IID (independent identically distributed) points.
The code below generates 4 Sobol samples of 2 dimensions.
distribution = Lattice(dimension=2, randomize=True, seed=7)
distribution.gen_samples(n_min=0,n_max=4)
array([[0.04386058, 0.58727432],
[0.54386058, 0.08727432],
[0.29386058, 0.33727432],
[0.79386058, 0.83727432]])
Multi-Dimensional Inputs
Suppose we want to create an integrand in QMCPy for evaluating the following integral:
![\int_{[0,1]^d} \|x\|_2^{\|x\|_2^{1/2}} dx,](../_images/math/6bf2402e203c2181888879db5e5139bd166e67f0.png)
where ![[0,1]^d](../_images/math/38fbdb5f0cd005023c1bb115f01c323f34f20446.png) is the unit hypercube in
is the unit hypercube in 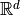 .
The integrand is defined everywhere except at
.
The integrand is defined everywhere except at 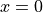 and hence the
definite integral is also defined.
and hence the
definite integral is also defined.
The key in defining a Python function of an integrand in the QMCPy
framework is that not only it should be able to take one point
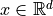 and return a real value, but also that it
would be able to take a set of
and return a real value, but also that it
would be able to take a set of 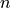 sampling points as rows in a
Numpy array of size
sampling points as rows in a
Numpy array of size 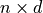 and return an array with
and return an array with
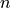 values evaluated at each sampling point. The following
examples illustrate this point.
values evaluated at each sampling point. The following
examples illustrate this point.
from numpy.linalg import norm as norm
from numpy import sqrt, array
Our first attempt maybe to create the integrand as a Python function as follows:
def f(x): return norm(x) ** sqrt(norm(x))
It looks reasonable except that maybe the Numpy function norm is executed twice. It’s okay for now. Let us quickly test if the function behaves as expected at a point value:
x = 0.01
f(x)
0.6309573444801932
What about an array that represents 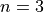 sampling points in a
two-dimensional domain, i.e.,
sampling points in a
two-dimensional domain, i.e., 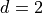 ?
?
x = array([[1., 0.],
[0., 0.01],
[0.04, 0.04]])
f(x)
1.001650000560437
Now, the function should have returned 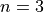 real values that
corresponding to each of the sampling points. Let’s debug our Python
function.
real values that
corresponding to each of the sampling points. Let’s debug our Python
function.
norm(x)
1.0016486409914407
Numpy’s norm(x) is obviously a matrix norm, but we want it to be
vector 2-norm that acts on each row of x. To that end, let’s add an
axis argument to the function:
norm(x, axis = 1)
array([1. , 0.01 , 0.05656854])
Now it’s working! Let’s make sure that the sqrt function is acting
on each element of the vector norm results:
sqrt(norm(x, axis = 1))
array([1. , 0.1 , 0.23784142])
It is. Putting everything together, we have:
norm(x, axis = 1) ** sqrt(norm(x, axis = 1))
array([1. , 0.63095734, 0.50502242])
We have got our proper function definition now.
def myfunc(x):
x_norms = norm(x, axis = 1)
return x_norms ** sqrt(x_norms)
We can now create an integrand instance with our QuickConstruct
class in QMCPy and then invoke QMCPy’s integrate function:
dim = 1
abs_tol = .01
integrand = CustomFun(
true_measure = Uniform(IIDStdUniform(dimension=dim, seed=7)),
g=myfunc)
solution,data = CubMCCLT(integrand,abs_tol=abs_tol,rel_tol=0).integrate()
print(data)
MeanVarData (AccumulateData Object)
solution 0.659
error_bound 0.010
n_total 4400
n 3376
levels 1
time_integrate 0.001
CubMCCLT (StoppingCriterion Object)
abs_tol 0.010
rel_tol 0
n_init 2^(10)
n_max 10000000000
inflate 1.200
alpha 0.010
CustomFun (Integrand Object)
Uniform (TrueMeasure Object)
lower_bound 0
upper_bound 1
IIDStdUniform (DiscreteDistribution Object)
d 1
entropy 7
spawn_key ()
For our integral, we know the true value. Let’s check if QMCPy’s solution is accurate enough:
true_sol = 0.658582 # In WolframAlpha: Integral[x**Sqrt[x], {x,0,1}]
abs_tol = data.stopping_crit.abs_tol
qmcpy_error = abs(true_sol - solution)
if qmcpy_error > abs_tol: raise Exception("Error not within bounds")
It’s good. Shall we test the function with 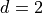 by simply
changing the input parameter value of dimension for QuickConstruct?
by simply
changing the input parameter value of dimension for QuickConstruct?
dim = 2
integrand = CustomFun(
true_measure = Uniform(IIDStdUniform(dimension=dim, seed=7)),
g = myfunc)
solution2,data2 = CubMCCLT(integrand,abs_tol=abs_tol,rel_tol=0).integrate()
print(data2)
MeanVarData (AccumulateData Object)
solution 0.831
error_bound 0.010
n_total 6659
n 5635
levels 1
time_integrate 0.002
CubMCCLT (StoppingCriterion Object)
abs_tol 0.010
rel_tol 0
n_init 2^(10)
n_max 10000000000
inflate 1.200
alpha 0.010
CustomFun (Integrand Object)
Uniform (TrueMeasure Object)
lower_bound 0
upper_bound 1
IIDStdUniform (DiscreteDistribution Object)
d 2^(1)
entropy 7
spawn_key ()
Once again, we could test for accuracy of QMCPy with respect to the true value:
true_sol2 = 0.827606 # In WolframAlpha: Integral[Sqrt[x**2+y**2])**Sqrt[Sqrt[x**2+y**2]], {x,0,1}, {y,0,1}]
abs_tol2 = data2.stopping_crit.abs_tol
qmcpy_error2 = abs(true_sol2 - solution2)
if qmcpy_error2 > abs_tol2: raise Exception("Error not within bounds")
