Elliptic PDE
import copy
import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt
from scipy.special import gamma, kv
from qmcpy.integrand._integrand import Integrand
from qmcpy.accumulate_data.mlmc_data import MLMCData
from qmcpy.accumulate_data.mlqmc_data import MLQMCData
import qmcpy as qp
# matplotlib options
rc_fonts = {
"text.usetex": True,
"font.size": 14,
"mathtext.default": "regular",
"axes.titlesize": 14,
"axes.labelsize": 14,
"legend.fontsize": 14,
"xtick.labelsize": 12,
"ytick.labelsize": 12,
"figure.titlesize": 16,
"font.family": "serif",
"font.serif": "computer modern roman",
}
mpl.rcParams.update(rc_fonts)
# set random seed for reproducability
np.random.seed(9999)
We will apply various multilevel Monte Carlo and multilevel quasi-Monte Carlo methods to approximate the expected value of a quantity of interest derived from the solution of a one-dimensional partial differential equation (PDE), where the diffusion coefficient of the PDE is a lognormal Gaussian random field. This example problem serves as an important benchmark problem for various methods in the uncertainty quantification and quasi-Monte Carlo literature. It is often referred to as the fruitfly problem of uncertainty quantification.
1. Problem definition
Let 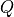 be a quantity of interest derived from the solution
be a quantity of interest derived from the solution
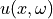 of the one-dimensional partial differential
equation (PDE)
of the one-dimensional partial differential
equation (PDE)
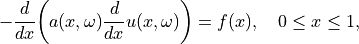
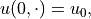
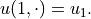
The notation 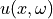 is used to indicate that the solution
depends on both the spatial variable
is used to indicate that the solution
depends on both the spatial variable 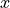 and the uncertain
parameter
and the uncertain
parameter 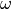 . This uncertainty is present because the
diffusion coefficient,
. This uncertainty is present because the
diffusion coefficient, 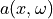 , is given by a lognormal
Gaussian random field with given covariance function. A common choice
for the covariance function is the so-called Matérn covariance function
, is given by a lognormal
Gaussian random field with given covariance function. A common choice
for the covariance function is the so-called Matérn covariance function
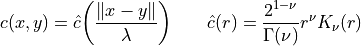
with 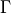 the gamma function and
the gamma function and 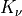 the Bessel
function of the second kind. This covariance function has two
parameters:
the Bessel
function of the second kind. This covariance function has two
parameters: 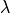 , the length scale, and
, the length scale, and 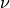 , the
smoothness parameter.
, the
smoothness parameter.
We begin by defining the Matérn covariance function Matern(x, y):
def Matern(x, y, smoothness=1, lengthscale=1):
distance = abs(x - y)
r = distance/lengthscale
prefactor = 2**(1-smoothness)/gamma(smoothness)
term1 = r**smoothness
term2 = kv(smoothness, r)
np.fill_diagonal(term2, 1)
cov = prefactor * term1 * term2
np.fill_diagonal(cov, 1)
return cov
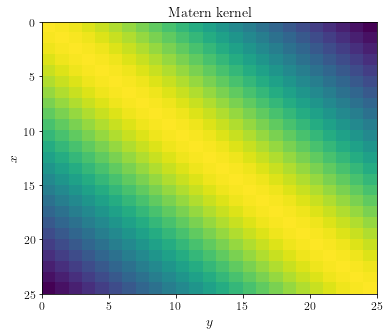
Let’s take a look at the covariance matrix obtained by evaluating the
covariance function in n=25 equidistant points in [0, 1].
def get_covariance_matrix(pts, smoothness=1, lengthscale=1):
X, Y = np.meshgrid(pts, pts)
return Matern(X, Y, smoothness, lengthscale)
n = 25
pts = np.linspace(0, 1, num=n)
fig, ax = plt.subplots(figsize=(6, 5))
ax.pcolor(get_covariance_matrix(pts).T)
ax.invert_yaxis()
ax.set_ylabel(r"$x$")
ax.set_xlabel(r"$y$")
ax.set_title(f"Matern kernel")
plt.show()
A lognormal Gaussian random field 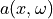 can be expressed
as
can be expressed
as 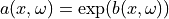 , where
, where 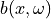 is a Gaussian random field. Samples of the Gaussian random field
is a Gaussian random field. Samples of the Gaussian random field
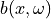 can be computed from a factorization of the
covariance matrix. Specifically, suppose we have a spectral (eigenvalue)
expansion of the covariance matrix
can be computed from a factorization of the
covariance matrix. Specifically, suppose we have a spectral (eigenvalue)
expansion of the covariance matrix 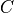 as
as
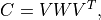
then samples of the Gaussian random field can be computed as
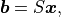
where 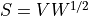 and
and 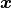 is a vector of
standard normal independent and identically distributed random
variables. This is easy to see, since
is a vector of
standard normal independent and identically distributed random
variables. This is easy to see, since
![\mathbb{E}[\boldsymbol{b}] = \mathbb{E}[S \boldsymbol{x}] = S\mathbb{E}[\boldsymbol{x}] = \boldsymbol{0}](../_images/math/6da9f4fda66bab3b33f6219eb7347284277989a2.png)
![\mathbb{E}[\boldsymbol{b} \boldsymbol{b}^T] = \mathbb{E}[S \boldsymbol{x} \boldsymbol{x}^T S^T] = S \mathbb{E}[\boldsymbol{x} \boldsymbol{x}^T] S^T = SS^T = VWV^T = C.](../_images/math/224e6c3c52b6bf89a91c4bd315f6e4a3afac0406.png)
First, let’s compute an eigenvalue decomposition of the covariance matrix.
def get_eigenpairs(n, smoothness=1, lengthscale=1):
h = 1/(n-1)
pts = np.linspace(h/2, 1 - h/2, num=n - 1)
cov = get_covariance_matrix(pts, smoothness, lengthscale)
w, v = np.linalg.eig(cov)
# ensure all eigenvectors are correctly oriented
for col in range(v.shape[1]):
if v[0, col] < 0:
v[:, col] *= -1
return pts, w, v
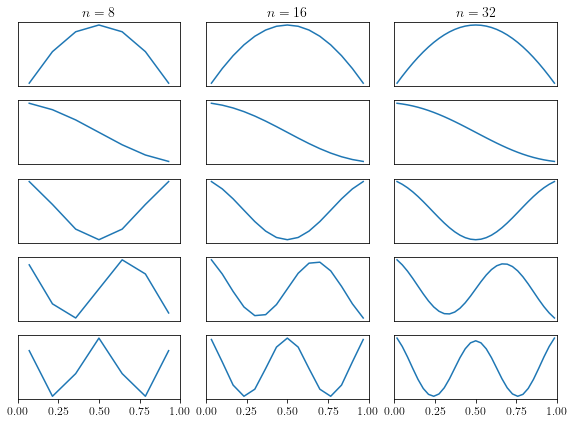
Next, we plot the eigenfunctions for different values of 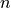 , the
number of grid points.
, the
number of grid points.
n = [8, 16, 32] # list of number of gridpoints to plot
m = 5 # number of eigenfunctions to plot
fig, axes = plt.subplots(m, len(n), figsize=(8, 6))
for j, k in enumerate(n):
x, w, v = get_eigenpairs(k)
for i in range(m):
axes[i, j].plot(x, v[:, i])
axes[i, j].set_xlim(0, 1)
axes[i, j].get_yaxis().set_ticks([])
if i < m - 1:
axes[i, j].get_xaxis().set_ticks([])
if i == 0:
axes[i, j].set_title(r"$n = " + repr(k) + r"$")
plt.tight_layout()
With this eigenvalue decomposition, we can compute samples of the
Gaussian random field 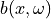 , and hence, also of the
lognormal Gaussian random field
, and hence, also of the
lognormal Gaussian random field
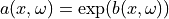 , since
, since
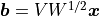 .
.
def evaluate(w, v, y=None):
if y is None:
y = np.random.randn(len(w) - 1)
m = len(y)
return v[:, :m] @ np.diag(np.sqrt(w[:m])) @ y
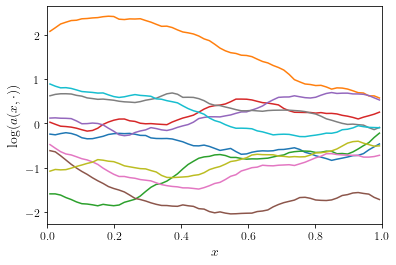
Let’s plot a couple of realizations of the Gaussian random field
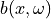 .
.
n = 64
x, w, v = get_eigenpairs(n)
fig, ax = plt.subplots(figsize=(6, 4))
for _ in range(10):
ax.plot(x, evaluate(w, v))
ax.set_xlim(0, 1)
ax.set_xlabel(r"$x$")
ax.set_ylabel(r"$\log(a(x, \cdot))$")
plt.show()
Now that we are able to compute realizations of the Gaussian random field, a next step is to compute a numerical solution of the PDE
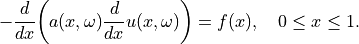
Using a straightforward finite-difference approximation, it is easy to
show that the numerical solution 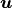 is the solution
of a tridiagonal system. The solutions of such a tridiagonal system can
be easily obtained in
is the solution
of a tridiagonal system. The solutions of such a tridiagonal system can
be easily obtained in 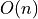 (linear) time using the tridiagonal
matrix algorithm (also known as the Thomas algorithm). More details can
be found
here.
(linear) time using the tridiagonal
matrix algorithm (also known as the Thomas algorithm). More details can
be found
here.
def thomas(a, b, c, d):
n = len(b)
x = np.zeros(n)
for i in range(1, n):
w = a[i-1]/b[i-1]
b[i] -= w*c[i-1]
d[i] -= w*d[i-1]
x[n-1] = d[n-1]/b[n-1]
for i in reversed(range(n-1)):
x[i] = (d[i] - c[i]*x[i+1])/b[i]
return x
For the remainder of this notebook, we will assume that the source term
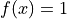 and Dirichlet boundary conditions
and Dirichlet boundary conditions
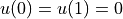 .
.
def pde_solve(a):
n = len(a)
b = np.full((n-1, 1), 1/n**2)
x = thomas(-a[1:n-1], a[:n-1] + a[1:], -a[1:n-1], b)
return np.insert(x, [0, n-1], [0, 0])
Let’s compute and plot a couple of solutions 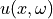 .
.
n = 64
_, w, v = get_eigenpairs(n)
x = np.linspace(0, 1, num=n)
fig, ax = plt.subplots(figsize=(6, 4))
for _ in range(10):
a = np.exp(evaluate(w, v))
u = pde_solve(a)
ax.plot(x, u)
ax.set_xlim(0, 1)
ax.set_xlabel(r"$x$")
ax.set_ylabel(r"$u(x, \cdot)$")
plt.show()
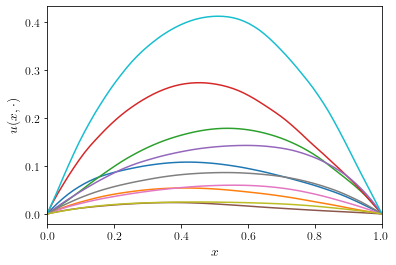
In the multilevel Monte Carlo method, we will rely on the ability to
generate “correlated” solutions of the PDE with varying mesh sizes. Such
a correlated solutions can be used as efficient control variates to
reduce the variance (or statistical error) in the approximation of the
expected value ![\mathbb{E}[Q]](../_images/math/bd4471fbcdd21becd1bfba267624c463d6ac4047.png) . Since we are using a factorization
of the covariance matrix to generate realizations of the Gaussian random
field, it is quite easy to obtain correlated samples: when sampling from
the “coarse” solution level, use the same set of random numbers used to
sample from the “fine” solution level, but truncated to the appropriate
size. Since the eigenvalue decomposition will reveal the most important
modes in the covariance matrix, that same eigenvalue decomposition on a
“coarse” approximation level will contain the same eigenfunctions,
represented on the coarse grid. Let’s illustrate this property on an
example using
. Since we are using a factorization
of the covariance matrix to generate realizations of the Gaussian random
field, it is quite easy to obtain correlated samples: when sampling from
the “coarse” solution level, use the same set of random numbers used to
sample from the “fine” solution level, but truncated to the appropriate
size. Since the eigenvalue decomposition will reveal the most important
modes in the covariance matrix, that same eigenvalue decomposition on a
“coarse” approximation level will contain the same eigenfunctions,
represented on the coarse grid. Let’s illustrate this property on an
example using n = 16 grid points for the fine solution level and
n = 8 grid points for the coarse solution level.
nf = 16
nc = nf//2
_, wf, vf = get_eigenpairs(nf)
_, wc, vc = get_eigenpairs(nc)
xf = np.linspace(0, 1, num=nf)
xc = np.linspace(0, 1, num=nc)
fig, ax = plt.subplots(figsize=(6, 4))
for _ in range(10):
yf = np.random.randn(nf - 1)
af = np.exp(evaluate(wf, vf, y=yf))
uf = pde_solve(af)
ax.plot(xf, uf)
yc = yf[:nc - 1]
ac = np.exp(evaluate(wc, vc, y=yc))
uc = pde_solve(ac)
ax.plot(xc, uc, color=ax.lines[-1].get_color(), linestyle="dashed", dash_capstyle="round")
ax.set_xlim(0, 1)
ax.set_ylim(bottom=0)
ax.set_xlabel(r"$x$")
ax.set_ylabel(r"$u(x, \cdot)$")
plt.show()
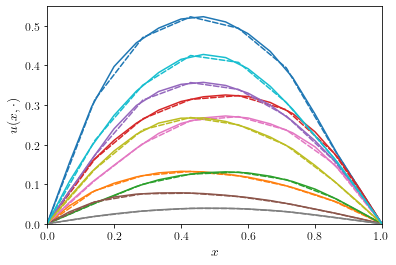
The better the coarse solution matches the fine grid solution, the more efficient the multilevel methods in Section 3 will perform.
2. Single-level methods
Let’s begin by using the single-level Monte Carlo and quasi-Monte Carlo
methods to compute the expected value ![\mathbb{E}[Q]](../_images/math/bd4471fbcdd21becd1bfba267624c463d6ac4047.png) . As quantity
of interest
. As quantity
of interest 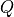 we take the solution of the PDE at
we take the solution of the PDE at 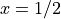 ,
i.e.,
,
i.e., 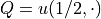 .
.
To integrate the elliptic PDE problem into QMCPy, we construct a
simple class as follows:
class EllipticPDE(Integrand):
def __init__(self, sampler, smoothness=1, lengthscale=1):
self.parameters = ["smoothness", "lengthscale", "n"]
self.smoothness = smoothness
self.lengthscale = lengthscale
self.n = len(sampler.gen_samples(n=1)[0]) + 1
self.compute_eigenpairs()
self.sampler = sampler
self.true_measure = qp.Gaussian(self.sampler)
super(EllipticPDE, self).__init__(dimension_indv=1,dimension_comb=1,parallel=False)
def compute_eigenpairs(self):
_, w, v = get_eigenpairs(self.n)
self.eigenpairs = w, v
def g(self, x):
n, d = x.shape
return np.array([self.__g(x[j, :].T) for j in range(n)])
def __g(self, x):
w, v = self.eigenpairs
a = np.exp(evaluate(w, v, y=x))
u = pde_solve(a)
return u[len(u)//2]
def _spawn(self, level, sampler):
return EllipticPDE(sampler, smoothness=self.smoothness, lengthscale=self.lengthscale)
# Custom print function
def print_data(data):
for key, val in vars(data).items():
kv = getattr(data, key)
if hasattr(kv, "parameters"):
print(f"{key}: {type(val).__name__}")
for param in kv.parameters:
print(f"\t{param}: {getattr(kv, param)}")
for param in data.parameters:
print(f"{param}: {getattr(data, param)}")
# Main function to test different methods
def test(problem, sampler, stopping_criterium, abs_tol=5e-3, verbose=True, **kwargs):
integrand = problem(sampler)
solution, data = stopping_criterium(integrand, abs_tol=abs_tol, **kwargs).integrate()
if verbose:
print(data)
print("\nComputed solution %.3f in %.2f s"%(solution, data.time_integrate))
Next, let’s apply simple Monte Carlo to approximate the expected value
![\mathbb{E}[Q]](../_images/math/bd4471fbcdd21becd1bfba267624c463d6ac4047.png) . The Monte Carlo estimator for
. The Monte Carlo estimator for
![\mathbb{E}[Q]](../_images/math/bd4471fbcdd21becd1bfba267624c463d6ac4047.png) is simply the sample average over a finite set of
samples, i.e.,
is simply the sample average over a finite set of
samples, i.e.,
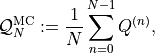
where 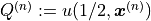 and we explicitly
denote the dependency of
and we explicitly
denote the dependency of 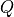 on the standard normal random numbers
on the standard normal random numbers
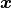 used to sample from the Gaussian random field. We
will continue to increase the number of samples
used to sample from the Gaussian random field. We
will continue to increase the number of samples 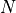 until a
certain error criterion is satisfied.
until a
certain error criterion is satisfied.
# MC
test(EllipticPDE, qp.IIDStdUniform(32), qp.CubMCCLT)
MeanVarData (AccumulateData Object)
solution 0.190
error_bound 0.005
n_total 19186
n 18162
levels 1
time_integrate 4.307
CubMCCLT (StoppingCriterion Object)
abs_tol 0.005
rel_tol 0
n_init 2^(10)
n_max 10000000000
inflate 1.200
alpha 0.010
EllipticPDE (Integrand Object)
smoothness 1
lengthscale 1
n 33
Gaussian (TrueMeasure Object)
mean 0
covariance 1
decomp_type PCA
IIDStdUniform (DiscreteDistribution Object)
d 2^(5)
entropy 326194454235761696154918970274080109080
spawn_key ()
Computed solution 0.190 in 4.31 s
The solution should be 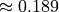 .
.
Similarly, the quasi-Monte Carlo estimator for ![\mathbb{E}[Q]](../_images/math/bd4471fbcdd21becd1bfba267624c463d6ac4047.png) is
defined as
is
defined as
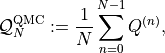
where 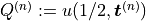 with
with
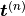 the
the 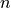 th low-discrepancy point
transformed to the distribution of interest. For our elliptic PDE, this
means that the quasi-Monte Carlo points, generated inside the unit cube
th low-discrepancy point
transformed to the distribution of interest. For our elliptic PDE, this
means that the quasi-Monte Carlo points, generated inside the unit cube
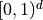 , are mapped to
, are mapped to 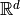 .
.
Because the quasi-Monte Carlo estimator doesn’t come with a reliable
error estimator, we run 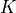 different quasi-Monte Carlo estimators
in parallel. The sample variance over these
different quasi-Monte Carlo estimators
in parallel. The sample variance over these 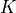 different
estimators can then be used as an error estimator.
different
estimators can then be used as an error estimator.
# QMC
test(EllipticPDE, qp.Lattice(32), qp.CubQMCCLT, n_init=32)
MeanVarDataRep (AccumulateData Object)
solution 0.189
comb_bound_low 0.185
comb_bound_high 0.192
comb_flags 1
n_total 2^(11)
n 2^(11)
n_rep 2^(7)
time_integrate 0.490
CubQMCCLT (StoppingCriterion Object)
inflate 1.200
alpha 0.010
abs_tol 0.005
rel_tol 0
n_init 2^(5)
n_max 2^(30)
replications 2^(4)
EllipticPDE (Integrand Object)
smoothness 1
lengthscale 1
n 33
Gaussian (TrueMeasure Object)
mean 0
covariance 1
decomp_type PCA
Lattice (DiscreteDistribution Object)
d 2^(5)
dvec [ 0 1 2 ... 29 30 31]
randomize 1
order natural
entropy 296354698279282161707952401923456574428
spawn_key ()
Computed solution 0.189 in 0.49 s
3. Multilevel methods
Implicit to the Monte Carlo and quasi-Monte Carlo methods above is a
discretization parameter used in the numerical solution of the PDE.
Let’s denote this parameter by 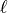 ,
, 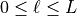 .
Multilevel methods are based on a telescopic sum expansion for the
expected value
.
Multilevel methods are based on a telescopic sum expansion for the
expected value ![\mathbb{E}[Q_L]](../_images/math/8a1466ed759e9861d57f93b2459e1918954e9f12.png) , as follows:
, as follows:
![\mathbb{E}[Q_L] = \mathbb{E}[Q_0] + \mathbb{E}[Q_1 - Q_0] + ... + \mathbb{E}[Q_L - Q_{L-1}].](../_images/math/7733584fedd029c68d4465ed696354d112818aa1.png)
Using a Monte Carlo method for each of the terms on the right hand side yields a multilevel Monte Carlo method. Similarly, using a quasi-Monte Carlo method for each term on the right hand side yields a multilevel quasi-Monte Carlo method.
3.1 Multilevel (quasi-)Monte Carlo
Our class EllipticPDE needs some changes to be integrated with the
multilevel methods in QMCPy.
class MLEllipticPDE(Integrand):
def __init__(self, sampler, smoothness=1, lengthscale=1, _level=None):
self.l = _level
self.parameters = ["smoothness", "lengthscale", "n", "nb_of_levels"]
self.smoothness = smoothness
self.lengthscale = lengthscale
dim = sampler.d + 1
self.nb_of_levels = int(np.log2(dim + 1))
self.n = [2**(l+1) + 1 for l in range(self.nb_of_levels)]
self.compute_eigenpairs()
self.sampler = sampler
self.true_measure = qp.Gaussian(self.sampler)
self.leveltype = "adaptive-multi"
self.sums = np.zeros(6)
self.cost = 0
super(MLEllipticPDE, self).__init__(dimension_indv=1,dimension_comb=1,parallel=False)
def _spawn(self, level, sampler):
return MLEllipticPDE(sampler, smoothness=self.smoothness, lengthscale=self.lengthscale, _level=level)
def compute_eigenpairs(self):
self.eigenpairs = {}
for l in range(self.nb_of_levels):
_, w, v = get_eigenpairs(self.n[l])
self.eigenpairs[l] = w, v
def g(self, x): # This function is called by keyword reference for the level parameter "l"!
n, d = x.shape
Qf = np.array([self.__g(x[j, :].T, self.l) for j in range(n)])
dQ = Qf
if self.l > 0: # Compute multilevel difference
dQ -= np.array([self.__g(x[j, :].T, self.l - 1) for j in range(n)])
self.update_sums(dQ, Qf)
self.cost = n*nf
return dQ
def __g(self, x, l):
w, v = self.eigenpairs[l]
n = self.n[l]
a = np.exp(evaluate(w, v, y=x[:n-1]))
u = pde_solve(a)
return u[len(u)//2]
def update_sums(self, dQ, Qf):
self.sums[0] = dQ.sum()
self.sums[1] = (dQ**2).sum()
self.sums[2] = (dQ**3).sum()
self.sums[3] = (dQ**4).sum()
self.sums[4] = Qf.sum()
self.sums[5] = (Qf**2).sum()
def _dimension_at_level(self, l):
return self.n[l]
Let’s apply multilevel Monte Carlo to the elliptic PDE problem.
test(MLEllipticPDE, qp.IIDStdUniform(32), qp.CubMCML)
MLMCData (AccumulateData Object)
solution 0.191
n_total 81898
levels 3
n_level [31258. 5902. 4173.]
mean_level [1.901e-01 6.267e-04 1.575e-04]
var_level [5.150e-02 3.690e-04 9.224e-05]
cost_per_sample [16. 16. 16.]
alpha 1.993
beta 2.000
gamma 2^(-1)
time_integrate 2.223
CubMCML (StoppingCriterion Object)
rmse_tol 0.002
n_init 2^(8)
levels_min 2^(1)
levels_max 10
theta 2^(-1)
MLEllipticPDE (Integrand Object)
smoothness 1
lengthscale 1
n [ 3 5 9 17 33]
nb_of_levels 5
Gaussian (TrueMeasure Object)
mean 0
covariance 1
decomp_type PCA
IIDStdUniform (DiscreteDistribution Object)
d 2^(5)
entropy 52139997603444977626041483839545508893
spawn_key ()
Computed solution 0.191 in 2.22 s
Now it’s easy to switch to multilevel quasi-Monte Carlo. Just change the
discrete distribution from IIDStdUniform to Lattice.
test(MLEllipticPDE, qp.Lattice(32), qp.CubQMCML, n_init=32)
MLQMCData (AccumulateData Object)
solution 0.190
n_total 74752
n_level [2048. 256. 32.]
levels 3
mean_level [ 1.900e-01 2.662e-05 -4.765e-05]
var_level [8.161e-07 4.455e-07 1.539e-07]
bias_estimate 2.06e-04
time_integrate 3.550
CubQMCML (StoppingCriterion Object)
rmse_tol 0.002
n_init 2^(5)
n_max 10000000000
replications 2^(5)
MLEllipticPDE (Integrand Object)
smoothness 1
lengthscale 1
n [ 3 5 9 17 33]
nb_of_levels 5
Gaussian (TrueMeasure Object)
mean 0
covariance 1
decomp_type PCA
Lattice (DiscreteDistribution Object)
d 2^(5)
dvec [ 0 1 2 ... 29 30 31]
randomize 1
order natural
entropy 119695915373660257480153154875270156239
spawn_key ()
Computed solution 0.190 in 3.55 s
3.2 Continuation multilevel (quasi-)Monte Carlo
In the continuation multilevel (quasi-)Monte Carlo method, we run the standard multilevel (quasi-)Monte Carlo method for a sequence of larger tolerances to obtain better estimates of the algorithmic parameters. The continuation multilevel heuristic will generally compute the same solution just a bit faster.
test(MLEllipticPDE, qp.IIDStdUniform(32), qp.CubMCMLCont)
MLMCData (AccumulateData Object)
solution 0.185
n_total 18182
levels 2^(2)
n_level [16273. 1288. 337. 256.]
mean_level [1.863e-01 1.710e-04 7.073e-04 2.501e-04]
var_level [5.082e-02 3.083e-04 2.395e-05 9.872e-07]
cost_per_sample [16. 16. 16. 16.]
alpha 2^(-1)
beta 4.143
gamma 2^(-1)
time_integrate 0.863
CubMCMLCont (StoppingCriterion Object)
rmse_tol 0.002
n_init 2^(8)
levels_min 2^(1)
levels_max 10
n_tols 10
tol_mult 1.668
theta_init 2^(-1)
theta 0.010
MLEllipticPDE (Integrand Object)
smoothness 1
lengthscale 1
n [ 3 5 9 17 33]
nb_of_levels 5
Gaussian (TrueMeasure Object)
mean 0
covariance 1
decomp_type PCA
IIDStdUniform (DiscreteDistribution Object)
d 2^(5)
entropy 56767261736751958322904251045568279667
spawn_key ()
Computed solution 0.185 in 0.86 s
test(MLEllipticPDE, qp.Lattice(32), qp.CubQMCMLCont, n_init=32)
MLQMCData (AccumulateData Object)
solution 0.189
n_total 41984
n_level [1024. 256. 32.]
levels 3
mean_level [ 1.891e-01 1.470e-04 -1.685e-04]
var_level [1.582e-06 7.087e-07 3.647e-07]
bias_estimate 4.66e-04
time_integrate 1.260
CubQMCMLCont (StoppingCriterion Object)
rmse_tol 0.002
n_init 2^(5)
n_max 10000000000
replications 2^(5)
levels_min 2^(1)
levels_max 10
n_tols 10
tol_mult 1.668
theta_init 2^(-1)
theta 0.058
MLEllipticPDE (Integrand Object)
smoothness 1
lengthscale 1
n [ 3 5 9 17 33]
nb_of_levels 5
Gaussian (TrueMeasure Object)
mean 0
covariance 1
decomp_type PCA
Lattice (DiscreteDistribution Object)
d 2^(5)
dvec [ 0 1 2 ... 29 30 31]
randomize 1
order natural
entropy 112259460192958188918668417604759964310
spawn_key ()
Computed solution 0.189 in 1.26 s
4. Convergence tests
Finally, we will run some convergence tests to see how these methods behave as a function of the error tolerance.
# Main function to test convergence for given problem
def test_convergence(problem, sampler, stopping_criterium, abs_tol=1e-3, verbose=True, smoothness=1, lengthscale=1, **kwargs):
integrand = problem(sampler, smoothness=smoothness, lengthscale=lengthscale)
stopping_crit = stopping_criterium(integrand, abs_tol=abs_tol, **kwargs)
# get accumulate_data
try:
stopping_crit.data = MLQMCData(stopping_crit, stopping_crit.integrand, stopping_crit.true_measure, stopping_crit.discrete_distrib, stopping_crit.levels_min, stopping_crit.levels_max, stopping_crit.n_init, stopping_crit.replications)
except:
stopping_crit.data = MLMCData(stopping_crit, stopping_crit.integrand, stopping_crit.true_measure, stopping_crit.discrete_distrib, stopping_crit.levels_min, stopping_crit.n_init, -1., -1., -1.)
# manually call "integrate()"
tol = []
n_samp = []
for t in range(stopping_crit.n_tols):
stopping_crit.rmse_tol = stopping_crit.tol_mult**(stopping_crit.n_tols-t-1)*stopping_crit.target_tol # update tol
stopping_crit._integrate() # call _integrate()
tol.append(copy.copy(stopping_crit.rmse_tol))
n_samp.append(copy.copy(stopping_crit.data.n_level))
if verbose:
print("tol = {:5.3e}, number of samples = {}".format(tol[-1], n_samp[-1]))
return tol, n_samp
# Execute the convergence test
def execute_convergence_test(smoothness=1, lengthscale=1):
# Convergence test for MLMC
tol_mlmc, n_samp_mlmc = test_convergence(MLEllipticPDE, qp.IIDStdUniform(32), qp.CubMCMLCont, verbose=False)
# Convergence test for MLQMC
tol_mlqmc, n_samp_mlqmc = test_convergence(MLEllipticPDE, qp.Lattice(32), qp.CubQMCMLCont, verbose=False, n_init=32)
# Compute cost per level
max_levels = max(max([len(n_samp) for n_samp in n_samp_mlmc]), max([len(n_samp) for n_samp in n_samp_mlqmc]))
cost_per_level = np.array([2**level + int(2**(level-1)) for level in range(max_levels)])
cost_per_level = cost_per_level/cost_per_level[-1]
# Compute total cost for each tolerance and store the result
cost = {}
cost["mc"] = (tol_mlmc, [n_samp_mlmc[tol][0] for tol in range(len(tol_mlmc))]) # where we assume V[Q_0] = V[Q_L]
cost["qmc"] = (tol_mlqmc, [n_samp_mlqmc[tol][0] for tol in range(len(tol_mlqmc))]) # where we assume V[Q_0] = V[Q_L]
cost["mlmc"] = (tol_mlmc, [sum([n_samp*cost_per_level[j] for j, n_samp in enumerate(n_samp_mlmc[tol])]) for tol in range(len(tol_mlmc))])
cost["mlqmc"] = (tol_mlqmc, [sum([n_samp*cost_per_level[j] for j, n_samp in enumerate(n_samp_mlqmc[tol])]) for tol in range(len(tol_mlqmc))])
return cost
# Plot the result
def plot_convergence(cost):
fig, ax = plt.subplots(figsize=(8, 6))
ax.plot(cost["mc"][0], cost["mc"][1], marker="o", label="MC")
ax.plot(cost["qmc"][0], cost["qmc"][1], marker="o", label="QMC")
ax.plot(cost["mlmc"][0], cost["mlmc"][1], marker="o", label="MLMC")
ax.plot(cost["mlqmc"][0], cost["mlqmc"][1], marker="o", label="MLQMC")
ax.legend(frameon=False)
ax.set_xscale("log")
ax.set_yscale("log")
ax.set_xlabel(r"error tolerance $\varepsilon$")
ax.set_ylabel(r"equivalent \# model evaluations at finest level")
plt.show()
This command takes a while to execute (about 1 minute on my laptop):
plot_convergence(execute_convergence_test())
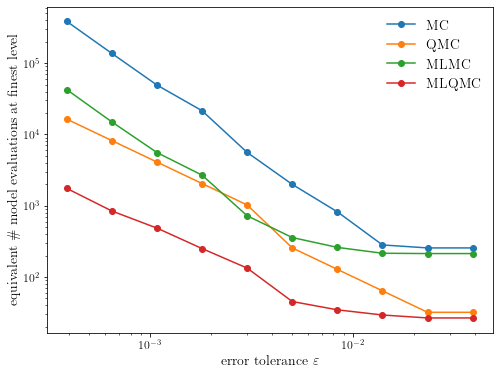
The benefit of the low-discrepancy point set depends on the smoothness
of the random field: the smoother the random field, the better. Here’s
an example for a Gaussian random field with a smaller smoothness
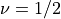 and smaller length scale
and smaller length scale 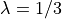 .
.
smoothness = 1/2
lengthscale = 1/3
n = 256
x, w, v = get_eigenpairs(n, smoothness=smoothness, lengthscale=lengthscale)
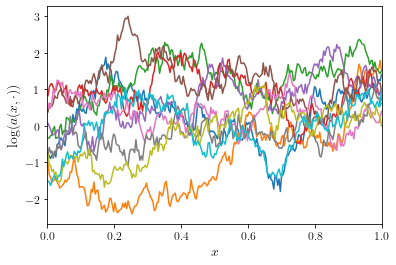
fig, ax = plt.subplots(figsize=(6, 4))
for _ in range(10):
ax.plot(x, evaluate(w, v))
ax.set_xlim(0, 1)
ax.set_xlabel(r"$x$")
ax.set_ylabel(r"$\log(a(x, \cdot))$")
plt.show()
plot_convergence(execute_convergence_test(lengthscale=lengthscale, smoothness=smoothness))
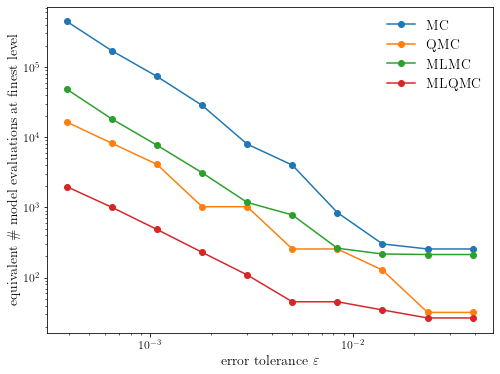
While the multilevel quasi-Monte Carlo method is still the fastest method, the asymptotic cost complexity of the QMC-based methods reduces to approximately the same rate as the MC-based methods.
The benefits of the multilevel methods over single-level methods will be even larger for two- or three-dimensional PDE problems, since it will be even more computationally efficient to take samples on a coarse grid.
