QMCPy for Lebesgue Integration

This notebook will give examples of how to use QMCPy for integration problems that not are defined in terms of a standard measure. i.e. Uniform or Gaussian.

from qmcpy import *
from numpy import *

Sample Problem 1

$y = \int_{[0,2]} x^2 dx, \:\: \mbox{Lebesgue Measure}$

$\phantom{y} = 2\int_{[0,2]} \frac{x^2}{2} dx, \:\: \mbox{Uniform Measure}$

abs_tol = .01
dim = 1
a = 0
b = 2
true_value = 8./3

# Lebesgue Measure
integrand = CustomFun(
    true_measure = Lebesgue(Uniform(Halton(dim, seed=7),lower_bound=a, upper_bound=b)),
    g = lambda x: (x**2).sum(1))
solution,data = CubQMCCLT(integrand, abs_tol=abs_tol).integrate()
print('y = %.3f'%solution)
error = abs((solution-true_value))
if error>abs_tol:
    raise Exception("Not within error tolerance")

y = 2.667

# Uniform Measure
integrand = CustomFun(
    true_measure = Uniform(IIDStdUniform(dim, seed=7), lower_bound=a, upper_bound=b),
    g = lambda x: (2*(x**2)).sum(1))
solution,data = CubMCCLT(integrand, abs_tol=abs_tol).integrate()
print('y = %.3f'%solution)
error = abs((solution-true_value))
if error>abs_tol:
    raise Exception("Not within error tolerance")

y = 2.666

Sample Problem 2

$y = \int_{[a,b]^d} ||x||_2^2 dx, \:\: \mbox{Lebesgue Measure}$

$\phantom{y} = \Pi_{i=1}^d (b_i-a_i)\int_{[a,b]^d} ||x||_2^2 \; [ \Pi_{i=1}^d (b_i-a_i)]^{-1} dx, \:\: \mbox{Uniform Measure}$

abs_tol = .001
dim = 2
a = array([1.,2.])
b = array([2.,4.])
true_value = ((a[0]**3-b[0]**3)*(a[1]-b[1])+(a[0]-b[0])*(a[1]**3-b[1]**3))/3
print('Answer = %.5f'%true_value)

Answer = 23.33333

# Lebesgue Measure
integrand = CustomFun(
    true_measure = Lebesgue(Uniform(DigitalNetB2(dim, seed=7), lower_bound=a, upper_bound=b)),
    g = lambda x: (x**2).sum(1))
solution,data = CubQMCCLT(integrand, abs_tol=abs_tol).integrate()
print('y = %.5f'%solution)
error = abs((solution-true_value))
if error>abs_tol:
    raise Exception("Not within error tolerance")

y = 23.33329

# Uniform Measure
integrand = CustomFun(
    true_measure = Uniform(DigitalNetB2(dim, seed=17), lower_bound=a, upper_bound=b),
    g = lambda x: (b-a).prod()*(x**2).sum(1))
solution,data = CubQMCCLT(integrand, abs_tol=abs_tol).integrate()
print('y = %.5f'%solution)
error = abs((solution-true_value))
if error>abs_tol:
    raise Exception("Not within error tolerance")

y = 23.33308

Sample Problem 3

Integral that cannot be done in terms of any standard mathematical functions

$y = \int_{[a,b]} \frac{\sin{x}}{\log{x}} dx, \:\: \mbox{Lebesgue Measure}$

Mathematica Code: Integrate[Sin[x]/Log[x], {x,a,b}]

abs_tol = .0001
dim = 1
a = 3
b = 5
true_value = -0.87961

# Lebesgue Measure
integrand = CustomFun(
    true_measure = Lebesgue(Uniform(Lattice(dim, randomize=True, seed=7),a,b)),
    g = lambda x: (sin(x)/log(x)).sum(1))
solution,data = CubQMCLatticeG(integrand, abs_tol=abs_tol).integrate()
print('y = %.3f'%solution)
error = abs((solution-true_value))
if error>abs_tol:
    raise Exception("Not within error tolerance")

y = -0.880

Sample Problem 4

Integral over 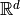$\mathbb{R}^d$

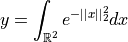
$y = \int_{\mathbb{R}^2} e^{-||x||_2^2} dx$

abs_tol = .1
dim = 2
true_value = pi

integrand = CustomFun(
    true_measure = Lebesgue(Gaussian(Lattice(dim,seed=7))),
    g = lambda x: exp(-x**2).prod(1))
solution,data = CubQMCLatticeG(integrand,abs_tol=abs_tol).integrate()
print('y = %.3f'%solution)
error = abs((solution-true_value))
if error>abs_tol:
    raise Exception("Not within error tolerance")

y = 3.142