Quasi-Monte Carlo Community Software

Quasi-Monte Carlo (QMC) methods are used to approximate multivariate integrals. They have four main components: an integrand, a discrete distribution, summary output data, and stopping criterion. Information about the integrand is obtained as a sequence of values of the function sampled at the data-sites of the discrete distribution. The stopping criterion tells the algorithm when the user-specified error tolerance has been satisfied. We are developing a framework that allows collaborators in the QMC community to develop plug-and-play modules in an effort to produce more efficient and portable QMC software. Each of the above four components is an abstract class. Abstract classes specify the common properties and methods of all subclasses. The ways in which the four kinds of classes interact with each other are also specified. Subclasses then flesh out different integrands, sampling schemes, and stopping criteria. Besides providing developers a way to link their new ideas with those implemented by the rest of the QMC community, we also aim to provide practitioners with state-of-the-art QMC software for their applications.

Homepage ~ Article ~ GitHub ~ Read the Docs ~ PyPI ~ Blogs ~ DockerHub ~ Contributing ~ Issues

Installation

pip install qmcpy

The QMCPy Framework

The central package including the 5 main components as listed below. Each component is implemented as abstract classes with concrete implementations. For example, the lattice and Sobol’ sequences are implemented as concrete implementations of the DiscreteDistribution abstract class. A complete list of concrete implementations and thorough documentation can be found in the QMCPy Read the Docs.

Stopping Criterion: determines the number of samples necessary to meet an error tolerance.
Integrand: the function/process whose expected value will be approximated.
True Measure: the distribution to be integrated over.
Discrete Distribution: a generator of nodes/sequences that can be either IID (for Monte Carlo) or low-discrepancy (for quasi-Monte Carlo), that mimic a standard distribution.
Accumulate Data: stores and updates data used in the integration process.

Quickstart

Note: If the following mathematics is not rendering try using Google Chrome and installing the Mathjax Plugin for GitHub.

We will approximate the expected value of the 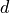$d$ dimensional Keister integrand [18]

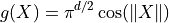
$g(X)=\pi^{d/2}\cos(\lVert X \rVert)$

where 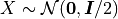$X \sim \mathcal{N}(\boldsymbol{0},\boldsymbol{I}/2)$ .

We may choose a Sobol’ discrete distribution with a corresponding Sobol’ cubature stopping criterion to preform quasi-Monte Carlo integration.

import qmcpy as qp
from numpy import pi, cos, sqrt, linalg
d = 2
dnb2 = qp.DigitalNetB2(d)
gauss_sobol = qp.Gaussian(dnb2, mean=0, covariance=1/2)
k = qp.CustomFun(
  true_measure = gauss_sobol,
  g = lambda x: pi**(d/2)*cos(linalg.norm(x,axis=1)))
qmc_sobol_algorithm = qp.CubQMCSobolG(k, abs_tol=1e-3)
solution,data = qmc_sobol_algorithm.integrate()
print(data)

Running the above code outputs

LDTransformData (AccumulateData Object)
    solution        1.808
    error_bound     4.68e-04
    n_total         2^(13)
    time_integrate  0.008
CubQMCSobolG (StoppingCriterion Object)
    abs_tol         0.001
    rel_tol         0
    n_init          2^(10)
    n_max           2^(35)
CustomFun (Integrand Object)
Gaussian (TrueMeasure Object)
    mean            0
    covariance      2^(-1)
    decomp_type     PCA
Sobol (DiscreteDistribution Object)
    d               2^(1)
    dvec            [0 1]
    randomize       LMS_DS
    graycode        0
    entropy         127071403717453177593768120720330942628
    spawn_key       ()

A more detailed quickstart can be found in our GitHub repo at QMCSoftware/demos/quickstart.ipynb or in this Google Colab quickstart notebook.

We also highly recommend you take a look at Fred Hickernell’s tutorial at the Monte Carlo Quasi-Monte Carlo 2020 Conference and the corresponding MCQMC2020 Google Colab notebook.

Community

Please refer to this document for the key roles in the QMCPy community.

Citation

If you find QMCPy helpful in your work, please support us by citing the following work:

Choi, S.-C. T., Hickernell, F. J., McCourt, M., Rathinavel, J. & Sorokin, A.
QMCPy: A quasi-Monte Carlo Python Library. Working. 2020.
https://qmcsoftware.github.io/QMCSoftware/

BibTex citation available here

## V id eo Tu to ri al Pl ea se r ef er to ` th is vi de o <h tt ps :/ /w ww .y ou tu be .c om /w at ch ?v =b Rc Ki LA 2y BQ >` __ f or a q ui ck in tr od uc ti on to QM CP y.

F or a mo re de ta il in tr od uc ti on r ef er to ` th is v id eo

<

ht tp s: // ww w. yo ut ub e. co m/ wa tc h? v= gL 8M _7 c- YU E> `_ _.

## Re fe re nc es

[ 1] F. Y. K uo a nd D. N uy en s. “A pp li ca ti on of q ua si -M on te C ar lo m et ho ds to el li pt ic PD Es wi th ra nd om d if fu si on co ef fi ci en ts - a su rv ey of an al ys is a nd im pl em en ta ti on ,” F ou nd at io ns of C om pu ta ti on al Ma th em at ic s, 16 (6 ): 16 31 -1 69 6, 2 01 6. (` sp ri ng er li nk

<

ht tp s: // li nk .s pr in ge r. co m/ ar ti cl e/ 10 .1 00 7/ s1 02 08 -0 16 -9 32 9- 5> `_ _, `a rx iv l in k <h tt ps :/ /a rx iv .o rg /a bs /1 60 6. 06 61 3> `_ _)

[ 2] Fr ed J. H ic ke rn el l, L an Ji an g, Yu ew ei Li u, a nd A rt B. O we n, “ Gu ar an te ed co ns er va ti ve f ix ed w id th co nf id en ce i nt er va ls v ia M on te C ar lo sa mp li ng ,” M on te C ar lo a nd Q ua si -M on te C ar lo M et ho ds 20 12 ( J. D ic k, F. Y. Ku o, G. W. P et er s, a nd I. H. Sl oa n, ed s. ), pp . 10 5- 12 8, Sp ri ng er -V er la g, B er li n, 2 01 4. DO I: 1 0. 10 07 /9 78 -3 -6 42 -4 10 95 -6 _5

[ 3] S ou -C he ng T. C ho i, Y uh an D in g, Fr ed J. H ic ke rn el l, L an Ji an g, L lu is An to ni J im en ez R ug am a, Da L i, J ag ad ee sw ar an R at hi na ve l, X in T on g, K an Zh an g, Y iz hi Zh an g, a nd Xu an Z ho u, G AI L: Gu ar an te ed A ut om at ic I nt eg ra ti on L ib ra ry (V er si on 2. 3. 1) [ MA TL AB So ft wa re ], 2 02 0. A va il ab le fr om ht tp :/ /g ai lg it hu b. gi th ub .i o/ GA IL _D ev /.

[ 4] S ou -C he ng T. C ho i, “ MI NR ES -Q LP Pa ck a nd Re li ab le Re pr od uc ib le Re se ar ch v ia S up po rt ab le Sc ie nt if ic So ft wa re ,” J ou rn al of Op en Re se ar ch S of tw ar e, Vo lu me 2, Nu mb er 1, e2 2, pp . 1- 7, 2 01 4.

[ 5] S ou -C he ng T. Ch oi a nd Fr ed J. H ic ke rn el l, “I IT MA TH -5 73 Re li ab le Ma th em at ic al S of tw ar e” [ Co ur se Sl id es ], Il li no is I ns ti tu te of T ec hn ol og y, Ch ic ag o, I L, 2 01 3. A va il ab le fr om ht tp :/ /g ai lg it hu b. gi th ub .i o/ GA IL _D ev /.

[ 6] Da ni el S. K at z, S ou -C he ng T. C ho i, Hi lm ar L ap p, K et an M ah es hw ar i, F ra nk Lo ff le r, M at th ew T ur k, Ma rc us D. Ha nw el l, N an cy Wi lk in s- Di eh r, J am es H et he ri ng to n, J am es Ho wi so n, Sh el Sw en so n, G ab ri el le D. Al le n, An ne C. E ls te r, B ru ce B er ri ma n, C ol in Ve nt er s, “S um ma ry of t he F ir st Wo rk sh op On S us ta in ab le So ft wa re f or Sc ie nc e: Pr ac ti ce a nd E xp er ie nc es ( WS SS PE 1) ,” J ou rn al of Op en Re se ar ch S of tw ar e, Vo lu me 2, Nu mb er 1, e 6, p p. 1 -2 1, 2 01 4.

[ 7] F an g, K. -T ., a nd W an g, Y. ( 19 94 ). Nu mb er -t he or et ic M et ho ds in S ta ti st ic s. L on do n, U K: C HA PM AN & HA LL

[ 8] L an Ji an g, Gu ar an te ed Ad ap ti ve M on te C ar lo M et ho ds f or Es ti ma ti ng M ea ns of Ra nd om Va ri ab le s, P hD T he si s, Il li no is I ns ti tu te of T ec hn ol og y, 2 01 6.

[ 9] L lu is An to ni J im en ez Ru ga ma a nd Fr ed J. H ic ke rn el l, “ Ad ap ti ve mu lt id im en si on al i nt eg ra ti on b as ed on ra nk -1 la tt ic es ,” M on te C ar lo a nd Q ua si -M on te C ar lo Me th od s: MC QM C, L eu ve n, Be lg iu m, A pr il 20 14 ( R. C oo ls a nd D. N uy en s, ed s. ), Sp ri ng er P ro ce ed in gs in M at he ma ti cs a nd S ta ti st ic s, v ol . 16 3, Sp ri ng er -V er la g, B er li n, 2 01 6, ar Xi v: 14 11 .1 96 6, pp . 40 7- 42 2.

[1 0] K ai -T ai Fa ng a nd Yu an W an g, Nu mb er -t he or et ic M et ho ds in S ta ti st ic s, C ha pm an & H al l, L on do n, 1 99 4.

[1 1] Fr ed J. Hi ck er ne ll a nd L lu is An to ni J im en ez R ug am a, “ Re li ab le ad ap ti ve cu ba tu re u si ng d ig it al s eq ue nc es ,” M on te C ar lo a nd Q ua si -M on te C ar lo Me th od s: MC QM C, L eu ve n, Be lg iu m, A pr il 20 14 ( R. C oo ls a nd D. N uy en s, ed s. ), Sp ri ng er P ro ce ed in gs in M at he ma ti cs a nd S ta ti st ic s, v ol . 16 3, Sp ri ng er -V er la g, B er li n, 2 01 6, a rX iv :1 41 0. 86 15 [m at h. NA ], pp . 36 7- 38 3.

[1 2] Ma ri us Ho fe rt a nd Ch ri st ia ne L em ie ux ( 20 19 ). q rn g: (R an do mi ze d) Qu as i- Ra nd om Nu mb er G en er at or s. R p ac ka ge v er si on 0. 0- 7. ht tp s: // CR AN .R -p ro je ct .o rg /p ac ka ge =q rn g.

[1 3] Fa ur e, He nr i, a nd Ch ri st ia ne Le mi eu x. “ Im pl em en ta ti on of I rr ed uc ib le So bo l’ S eq ue nc es in P ri me P ow er B as es ,” M at he ma ti cs a nd C om pu te rs in Si mu la ti on 1 61 ( 20 19 ): 13 –2 2.

[1 4] M. B. Gi le s. “M ul ti -l ev el M on te C ar lo pa th si mu la ti on ,” Op er at io ns R es ea rc h, 56 (3 ): 60 7- 61 7, 2 00 8. h tt p: // pe op le .m at hs .o x. ac .u k/ ~g il es m/ fi le s/ OP RE _2 00 8. pd f.

[1 5] M. B. Gi le s. “ Im pr ov ed mu lt il ev el M on te C ar lo c on ve rg en ce u si ng t he Mi ls te in sc he me ,” 34 3- 35 8, in M on te C ar lo a nd Q ua si -M on te C ar lo M et ho ds 2 00 6, S pr in ge r, 2 00 8. h tt p: // pe op le .m at hs .o x. ac .u k/ ~g il es m/ fi le s/ mc qm c0 6. pd f.

[1 6] M. B. G il es a nd B. J. W at er ho us e. “ Mu lt il ev el q ua si -M on te C ar lo pa th si mu la ti on ,” pp .1 65 -1 81 in Ad va nc ed F in an ci al Mo de ll in g, in R ad on Se ri es on C om pu ta ti on al a nd A pp li ed Ma th em at ic s, de Gr uy te r, 2 00 9. h tt p: // pe op le .m at hs .o x. ac .u k/ ~g il es m/ fi le s/ ra do n. pd f.

[1 7] O we n, A. B. “A ra nd om iz ed Ha lt on a lg or it hm in R ,” 2 01 7. ar Xi v: 17 06 .0 28 08 [ st at .C O]

[1 8] B. D. Ke is te r, Mu lt id im en si on al Qu ad ra tu re A lg or it hm s, ‘C om pu te rs in P hy si cs ’, 1 0, pp . 11 9- 12 2, 1 99 6.

[1 9] L ’E cu ye r, Pi er re & M un ge r, Da vi d. ( 20 15 ). L at ti ce Bu il de r: A G en er al So ft wa re To ol f or Co ns tr uc ti ng Ra nk -1 L at ti ce Ru le s. A CM Tr an sa ct io ns on Ma th em at ic al S of tw ar e. 4 2. 10 .1 14 5/ 27 54 92 9.

[2 0] Fi sc he r, G re go ry & C ar mo n, Z iv & Za ub er ma n, G al & L ’E cu ye r, P ie rr e. ( 19 99 ). Go od Pa ra me te rs a nd I mp le me nt at io ns f or Co mb in ed Mu lt ip le R ec ur si ve Ra nd om Nu mb er G en er at or s. Op er at io ns R es ea rc h. 4 7. 15 9- 16 4. 10 .1 28 7/ op re .4 7. 1. 15 9.

[2 1] I. M. S ob ol ’, V. I. Tu rc ha ni no v, Y u. L. Le vi ta n, B. V. S hu kh ma n: “ Qu as i- Ra nd om Se qu en ce G en er at or s” K el dy sh I ns ti tu te of A pp li ed Ma th em at ic s, R us si an A ca md ey of S ci en ce s, Mo sc ow ( 19 92 ).

[2 2] So bo l, Il ya & As ot sk y, D an il & Kr ei ni n, A le xa nd er & K uc he re nk o, S er ge i. ( 20 11 ). Co ns tr uc ti on a nd Co mp ar is on of Hi gh -D im en si on al So bo l’ G en er at or s. Wi lm ot t. 2 01 1. 1 0. 10 02 /w il m. 10 05 6.

[2 3] P as zk e, A ., Gr os s, S ., Ma ss a, F ., Le re r, A ., B ra db ur y, J ., C ha na n, G ., … C hi nt al a, S. ( 20 19 ). Py To rc h: An Im pe ra ti ve St yl e, Hi gh -P er fo rm an ce De ep Le ar ni ng Li br ar y. In H. Wa ll ac h, H. L ar oc he ll e, A. Be yg el zi me r, F. d ex tq uo te si ng le A lc h’ e- Bu c, E. Fo x, & R. G ar ne tt ( Ed s. ), Ad va nc es in Ne ur al I nf or ma ti on Pr oc es si ng S ys te ms 32 (p p. 8 02 4– 80 35 ). Cu rr an A ss oc ia te s, In c. R et ri ev ed fr om ht tp :/ /p ap er s. ne ur ip s. cc /p ap er /9 01 5- py to rc h- an -i mp er at iv e- st yl e- hi gh -p er fo rm an ce -d ee p- le ar ni ng -l ib ra ry .p df

[2 4] S. J oe a nd F. Y. Ku o, Co ns tr uc ti ng S ob ol s eq ue nc es wi th be tt er t wo -d im en si on al pr oj ec ti on s, SI AM J. Sc i. C om pu t. 3 0, 2 63 5- 26 54 ( 20 08 ).

[2 5] Pa ul B ra tl ey a nd B en ne tt L. Fo x. 1 98 8. A lg or it hm 65 9: Im pl em en ti ng S ob ol ’s q ua si ra nd om se qu en ce ge ne ra to r. A CM Tr an s. M at h. So ft w. 1 4, 1 (M ar ch 19 88 ), 8 8– 10 0. DO I: ht tp s: // do i. or g/ 10 .1 14 5/ 42 28 8. 21 43 72

[2 6] P. L ’E cu ye r, P. M ar io n, M. Go di n, a nd F. P uc hh am me r, “A To ol f or Cu st om Co ns tr uc ti on of Q MC a nd RQ MC P oi nt Se ts ,” M on te C ar lo a nd Q ua si -M on te C ar lo M et ho ds 2 02 0.

[2 7] P Ku ma ra sw am y, A g en er al iz ed p ro ba bi li ty d en si ty fu nc ti on f or do ub le -b ou nd ed ra nd om pr oc es se s. J. H yd ro l. 4 6, 7 9– 88 ( 19 80 ).

[2 8] D L i, Re li ab le q ua si -M on te C ar lo wi th c on tr ol v ar ia te s. Ma st er ’s t he si s, Il li no is I ns ti tu te of Te ch no lo gy (2 01 6)

[2 9] D. H. B ai le y, J. M. Bo rw ei n, R. E. C ra nd al l, B ox in te gr al s, J ou rn al of C om pu ta ti on al a nd A pp li ed Ma th em at ic s, Vo lu me 20 6, I ss ue 1, 2 00 7, P ag es 19 6- 20 8, IS SN 03 77 -0 42 7, ht tp s: // do i. or g/ 10 .1 01 6/ j. ca m. 20 06 .0 6. 01 0.

[3 0] A rt B. Ow en .M on te C ar lo t he or y, m et ho ds a nd e xa mp le s. 2 01 3.

Sponsors

Illinois Tech
Kamakura Corporation, acquired by SAS Institute Inc. in June 2022
SigOpt, Inc.